Y=ax^2 parabola 483697-Y=ax^2 parabola

 The graph of a quadratic equation in two variables (y = ax 2 bx c) is called a parabola Furthermore, how do you find the Y intercept of ax 2 bx c? It would be worth your while to learn another standard form of the equation of a parabola, and you can complete the square, given $y = ax^2 bx c$, to obtain this form $$4p(y k) = (xh)^2$$ The vertex of the parabola is given by $(h, k)$ $$h = \frac{b}{2a};\quad k = \frac{4ac b^2}{4a}$$The Graph of y = ax2 bx c 393 Lesson 64 The Graph of y = ax2 bx c Lesson 6–4 2 BIG IDEA The graph of y = ax bx c, a ≠ 0, is a parabola that opens upward if a > 0 and downward if a < 0 Standard Form for the Equation of a Parabola Homer King hits a high–fl y

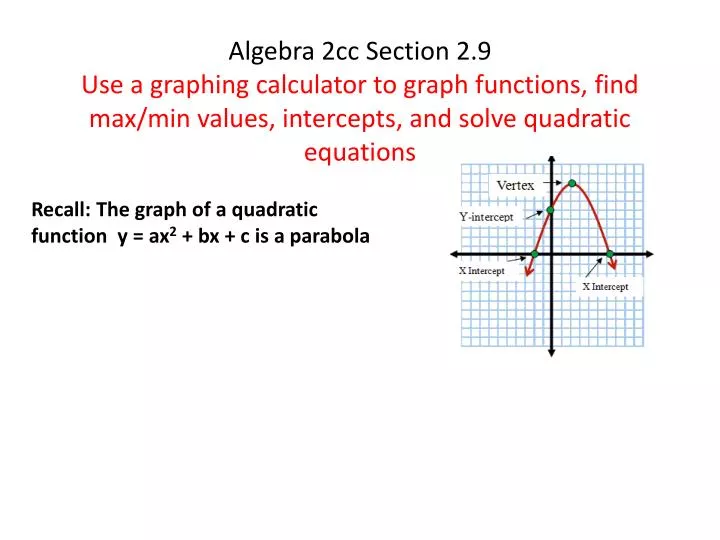
Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id

Y=ax^2 parabola

Y=ax^2 parabola-Find the yintercept for the equation by letting x equal zero The equation becomes y = 0x squared 0x c or y = c Note that the yintercept of a quadratic equation written in the form y = axIn the next few questions, we will find the roots of the general equation y = a x 2 b x with a ≠ 0 by factoring, and use that to get a formula for the axis of symmetry of any equation in that form Question 5 We want to factor a x 2 b x Because both terms contain an x,

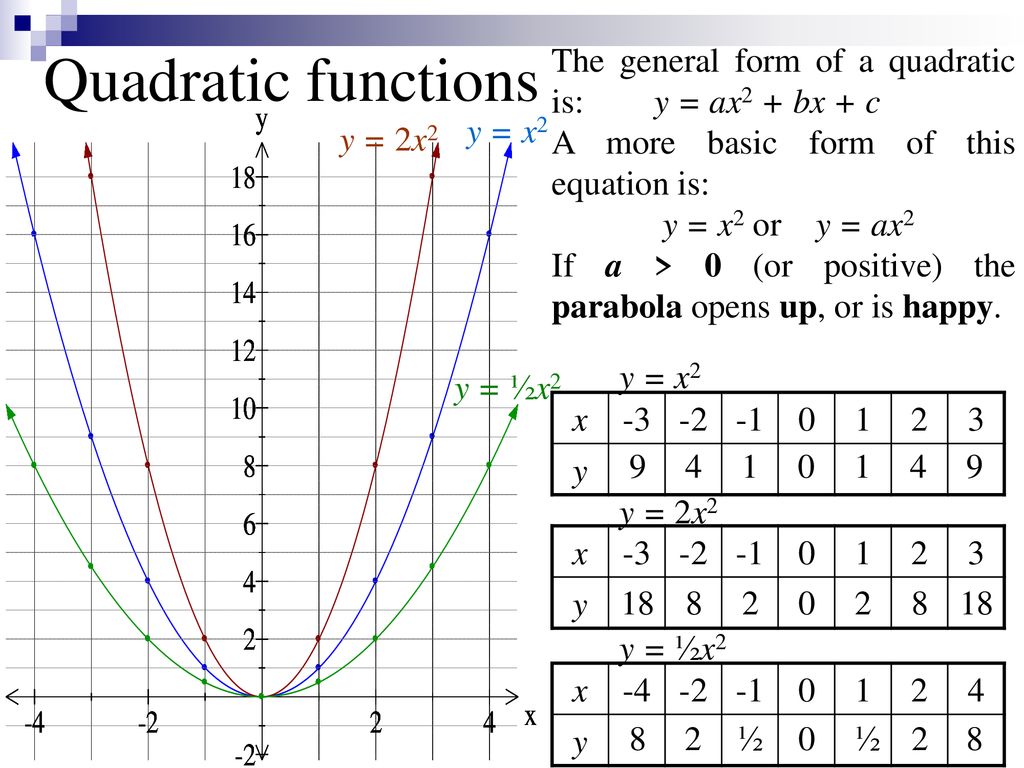
Quadratic Functions The General Form Of A Quadratic Is Y Ax2 Bx C A More Basic Form Of This Equation Is Y X2 Or Y Ax2 If

 First complete the square to get the form y = a(x − h)2 k where again a ≠ 0 Then show that this is also the equation for the parabola with its focus at the point (h, k 1 4a) and directrix at the horizontal line y = k − 1 4a These are welldefined since a ≠ 0 and clearly the focus is not on the directrix Given the Equation #color(red)(y=f(x)=4x^2# A Quadratic Equation takes the form #color(blue)(y=ax^2bxc# Graph of a quadratic function forms a Parabola The coefficient of the #color(red)(x^2# term (a) makes the parabola wider or narrow If the coefficient of the #color(red)(x^2,# term (a) is negative then the parabola opens down The term Vertex is usedI mean, given the focus x, y and directrix (I'll use a horizontal line for simplicity) y = k you can find the equation of the quadratic;

Http//wwwlezionidimateit http//wwwwikimateit In questa lezione cominciamo a definire la parabola e successivamente trattiamo il caso specifico di una p A parabola y = ax 2 bx c crosses the x axis at (α, 0) (β, 0) both to the right of the originA circle also passes through these two points The graph of a quadratic function is a parabola The parabola can either be in "legs up" or "legs down" orientation We know that a quadratic equation will be in the form y = ax 2 bx c Our job is to find the values of a, b and c after first observing the graph

The general form of a quadratic is "y = ax 2 bx c" For graphing, the leading coefficient " a " indicates how "fat" or how "skinny" the parabola will be For a > 1 (such as a = 3 or a = –4 ), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample valuesFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceFor example, a univariate quadratic function has the form f = a x 2 b x c, a ≠ 0 {\displaystyle f=ax^{2}bxc,\quad a\neq 0} in the single variable x The graph of a univariate quadratic function is a parabola whose axis of symmetry is parallel to the yaxis, as shown at right If the quadratic function is set equal to zero, then the result is a quadratic equation The solutions to the

Chapter 9 Quadratic Functions And Equations Flashcards Quizlet

1

Parabolas The graph of a quadratic equation in two variables (y = ax2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot We say that the first parabola opens upwards (is a U shape) and the second parabola(a = 1) y = 1/2x 2 (a = 1/2) y = 4x 2 (a = 4) y = 25x 2 1 (a = 25) Change a, Change the GraphDunque, anche il grafico della funzione y=ax 2 bxc è una parabola, tuttavia mentre la parabola di equazione y=ax 2 ha vertice nell'origine e asse coincidente con l'asse y, la parabola di, la parabola y=ax 2 bxc può avere il vertice in un punto qualsiasi del piano cartesiano e ha l'asse parallelo (ma non necessariamente coincidente) all

Sat Math Multiple Choice Question 2 Answer And Explanation Cracksat Net

Sat Math Grid Ins Question 97 Answer And Explanation Cracksat Net

Click here👆to get an answer to your question ️ If the parabola y = ax^2 6x b passes through (0, 2) and has its tangent at x = 32 parallel to the x axis thenThe form y = ax 2 bx c provides the yintercept of the graph, the point (0, c), and the quadratic formula is based in the values of a, b, and c to find the zeros of the graph Example The graph of y = 2x 2 4x 6 has yintercept (0, 6) and using the quadratic formula its zeros areWhen first looking at the equation y = ax^2 we know that we will be graphing a parabola A parabola is the set of all points that are the same distance from a fixed line called the directrix and a fixed point called the focus, that is not located on the directrix

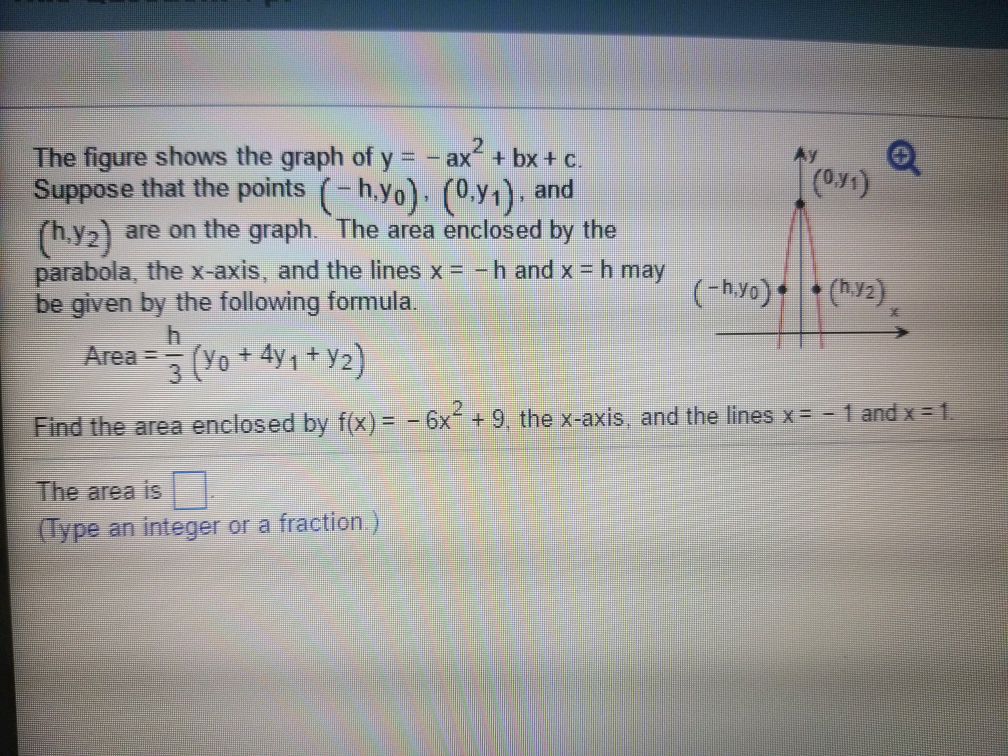
The Figure Shows The Graph Of Y Ax 2 Bx C Chegg Com

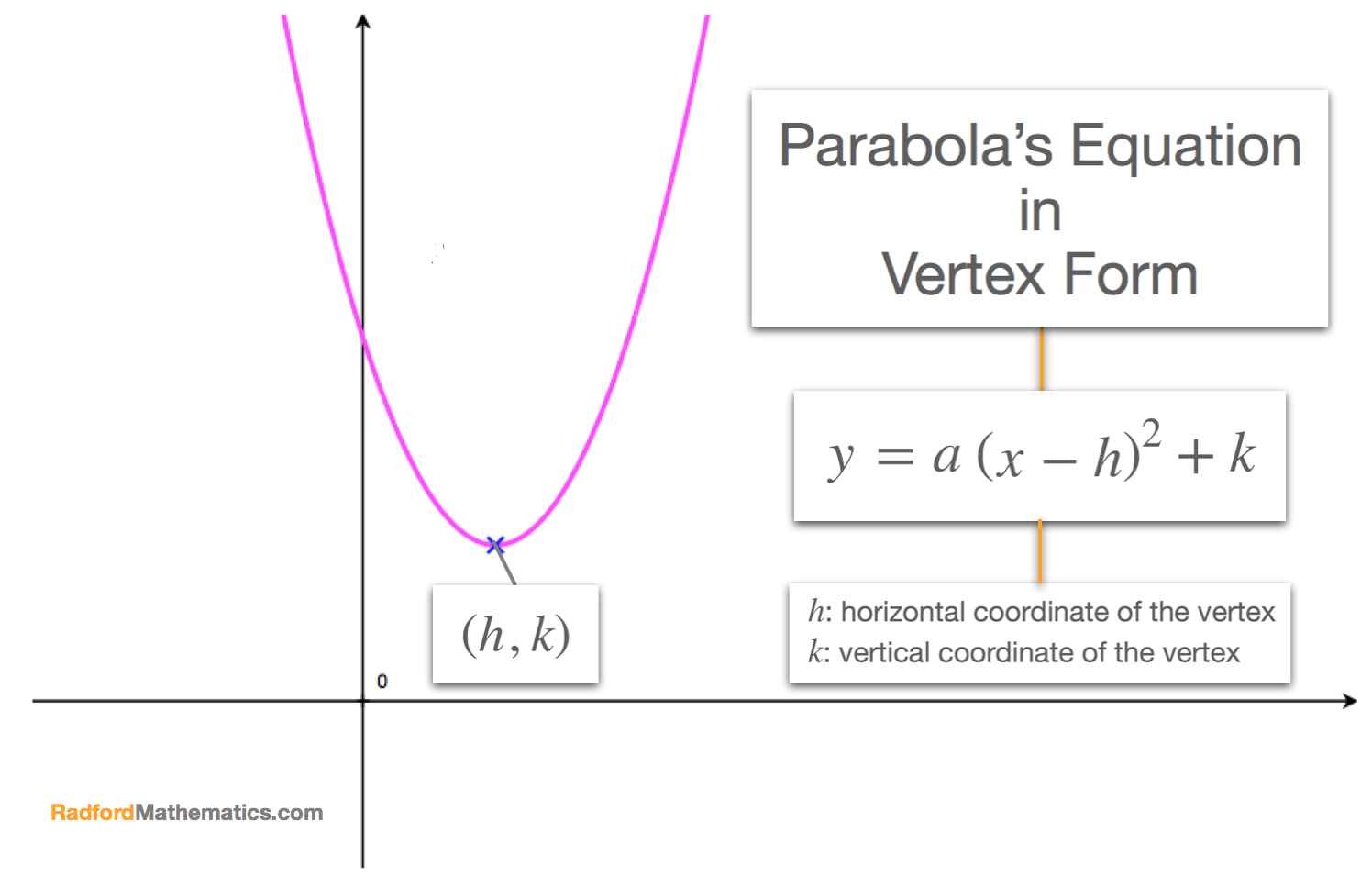
Vertex Form How To Find The Equation Of A Parabola

 Step 1, Accept a parabola in standard formula format, ie y = ax^2 bx cStep 2, Find the following elements, which you also memorize the methods or formulas for per the following KEY Determine whether element a of the equation is positive and the parabola has a minimum and opens up, or a is negative, and the parabola has a maximum and opens down Find the Axis of Symmetry, which = b/2a Find the parabola's Best Answer Suppose that we have an equation y=ax^2bxc whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0)How do you do this backwards?

How To Analyze A Parabola 6 Steps With Pictures Wikihow

The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com

If the parabola \(y = 3x^2 1\) is shifted \(\text{2}\) units to the right, determine the equation of the new parabola Carl's answer A shift to the right means moving in the positive \(x\) direction, therefore \(x\) is replaced with \(x 2\) and the new equation is \(y = 3(x 2)^2 1\) Eric's answer 2 How can you find the directrix and focus of a parabola (quadratic function) a x 2 b x c, where a ≠ 0?Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis

Quadratic Systems A Line And A Parabola Video Khan Academy

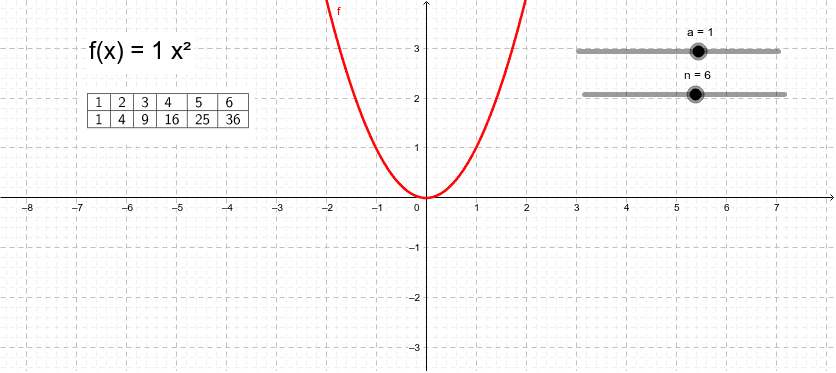
Parabola Y Ax 2 Geogebra

1234567891011Next

Incoming Term: y=ax^2 parabola, y=ax^2+bx+c parabola, a parabola y=ax^2+bx+c crosses the x axis, the parabola y=ax^(2)+2ax+b is symmetric about the line, parabola equation y=ax^2, parabola form y=ax^2, focus of parabola y=ax^2+bx+c, vertex of parabola y=ax^2+bx+c, if the parabola y=ax^2-6x+b, if the parabola y=ax^2+bx+c,