Explanation Step 1 1 of 3 x 2 b x − 24 x^2bx24 x 2 b x − 24 The given expression is completely factorizable if we can find two integers such that their sum is b b b and their product is 24 Following are the total number of ways in which we can write 24 as a product of two numbers 23 Solving Linear Equations Part 1 Identify linear equations with one variable and verify their solutions Use the properties of equality to solve basic linear equations Use multiple steps to solve linear equations by isolating the variable Solve linear equations where the coefficients are fractions or decimals Misc 5 Solve the inequality −12 < 4 −3𝑥/(−5) ≤ 2 −12 < 4 −3𝑥/(−5) ≤ 2 Subtracting 4 all sides (Eliminating 4) – 12 – 4 < 4 − 3𝑥/(−5

Graphing Parabolas
3x+5-2(x+2)=8-3(1-x)
3x+5-2(x+2)=8-3(1-x)-SOLUTION by C2→ C2−C1 C3→ C3−4C1 =−(−x−2x)1(−2x−43x)x(2−3) =2x−4−x= −2 Trick Put x = 1 Then ∣∣ ∣ ∣2 3 5 4 6 9 8 11 15∣∣ ∣ ∣= −2Quadratic polynomial can be factored using the transformation a x 2 b x c = a (x − x 1 ) (x − x 2 ), where x 1 and x 2 are the solutions of the quadratic equation a x 2 b x c = 0 3x^{2}5x1=0
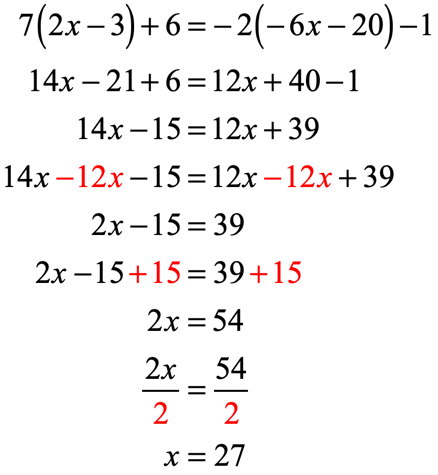



Distributive Property Chilimath
D) −5sin(5x)5ex1 − 14 3 3 √ x−1; Solve the compound inequality Graph the solution and write the solution in interval notation 1 5x − 5 ≥ − 3 and − 4(x − 1) ≥ − 2 Answer Sometimes we have a compound inequality that can be written more concisely For example, a < x and x < b can be written simply as a < x < b and then we call it a double inequality5 a 5 6 a 1 2 − = 6 x 3 x x 1 x 3x 1 2 − = − − D Absolute value 1 5−2z −1=8 2 x5 −7 =−2 3 5x −1 =−2 4 4 1 4 3 x 2 1 − = 5 y −1 =7 y E Exponential 1 10x =1000 2 103x5 =100 3 8 1 2x1 = 4 () 3 1 3x2 9x = 5 () 8 1 2 2 42x = F Logarithmic 1 log2 ( )x 5 =log2 1−5x 2 2log3 ()x 1 =log3 4x 3 log2 ()x
Step 2 Use the appropriate properties of equality to combine oppositeside like terms with the variable term on one side of the equation and the constant term on the other Step 3 Divide or multiply as needed to isolate the variable Step 4 Check to see if the answer solves the original equationThe sum of these coefficients is 0 and thus the elimination method can be applied directly Step 3 3 of 5 Next, we subtract the two equations This will eliminate \textbf {eliminate} eliminate one of the variables We solve the equation to the other (uneliminated) variable ( 3 x − 2 y) − ( 2 x − 2 y) = 8 − 5 (3x2y) (2x2y)=85Click here👆to get an answer to your question ️ Find the value of the polynomial 3x^3 4x^2 7x 5, when x = 3 and also when x = 3 Join / Login Question Find the value of the polynomial 3 x 3 = 8 1 − 3 6 2 1 − 5 = 6 1
B) 3 6 2 29 3x − = ;A)10 53 7( 3) 1525 ( 9)−− ;3x1=x8 One solution was found x = 9/2 = 4500 Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation




Example 13 Solve 5x 7 2 3 2 X 14 Chapter 2 Class 8




Polynomials Exercise 2 3 Class 10 Breath Math
Answer to − 5(x 2) 8x = − 2 3x − 8 Find solutions for your homework or get textbooks SearchA) (−5, −2) B) (3, −8) C) (4, −6) D) (9, −6) 534 views Share FollowX∞ n=1 5−2 √ n n3 We can temporarily break this apart to see if the pieces converge X∞ n=1 5−2 √ n n3 = X∞ n=1 5 n3 −2 X∞ n=1 √ n n3 Both of these are p−series, the first with p = 3, the second with p = 5 2, therefore they converge separately, and so the sum also converges 5 X∞ n=1 (−6)n−151−n First, let's



What Is The Solution To The Equation 1 2x 3 2 X 1 1 4 5 Quora




Differentiation Using The Chain Rule
A 3x 3 −10 B −3x 2 x−7 C 3x 3 −6x 2 5x−10 D 3x 2 −x7 Given f(x)=2x 2 −5x−3 and g(x)=2x 2 x What is (fg)(x) ?A x 8 B 3x 8 C x − 2 D x − 8 2 See answers Advertisement Advertisement Transcript Ex 93, 4 (a) (a) Simplify 3x (4x – 5) 3 and find its values for (i) x = 3 (ii) x = 1/2 3𝑥 (4𝑥−5)3 = (3𝑥×4𝑥)−(3𝑥×5)3 = 12𝑥^2−15𝑥3 (i) For 𝒙=𝟑 Putting 𝑥=3 in expression 12𝑥^2−15𝑥3 = 12(3)^2−15(3)3 = (12×9)−(15×3) 3 = 108−45 3 = 108−42 = 66 (ii) For 𝒙=𝟏/𝟐 Putting 𝑥=1/2 in expression 12𝑥^2−15𝑥3




Find The Derivative For The Following Functions Find Chegg Com




Solve Solve Inequalities With Step By Step Math Problem Solver
2(42x)≥5x5 x≤−2 x≥−2 x≤3 x≥3 2 See answers Advertisement Advertisement carlenehagen carlenehagen 8 4x >_ 5x 5,,, 3 >_ x (>_ just means greater than our equal to) Advertisement Advertisement krislynnkat krislynnkat X is less then of equal to 3 Answer x = 0 For the functions f ( x) in exercises 6 10, determine whether there is an asymptote at x = a Justify your answer without graphing on a calculator 6) f ( x) = x 1 x 2 5 x 4, a = − 1 7) f ( x) = x x − 2, a = 2 Answer Yes, there is a vertical asymptote at x = 2 8) f ( x) = ( x 2) 3 / 2, a = − 2Combine 4 x 2 and − 5 x 2 to get − x 2 Add 9 and to get 29 Add 9 and 2 0 to get 2 9 Multiply 2x3 and 2x3 to get \left (2x3\right)^ {2} Multiply 2 x − 3 and 2 x − 3 to get ( 2 x − 3) 2 Use binomial theorem \left (ab\right)^ {2}=a^ {2}2abb^ {2} to expand \left (2x3\right)^ {2}
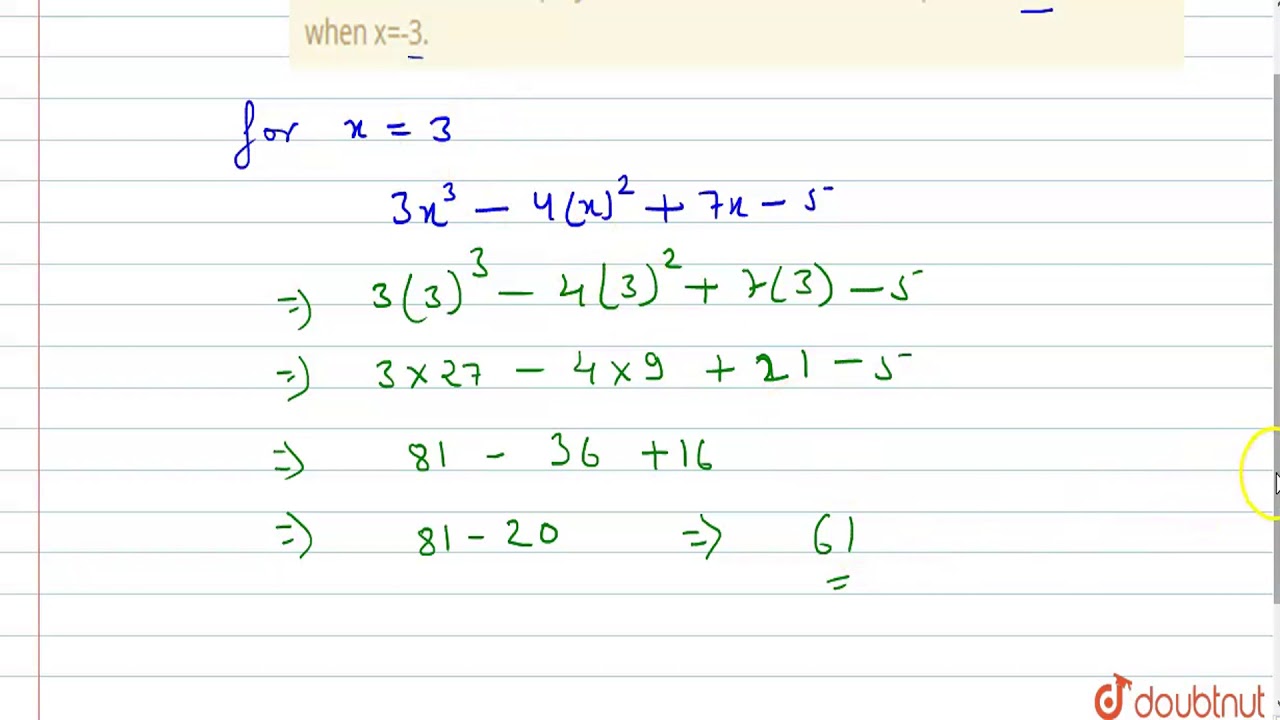



Find The Value Of The Polynomial 3x 3 4x 2 7x 5 When X 3 And Also When X 3 Youtube




Factoring Calculator Wolfram Alpha
3cos(5x)2ln(4x)8 √ x 5 f) cos(4x)3ln(3x)−7 5 √ x 3 g) 4sin(3x)3ln(x)− √6 x −1 2 h) 4sin(5x)e3x − 4 √ 4 x 5 2 Answers a) 25cos(5x)16e4x1 − 2 x 3/2;Explanation Step 1 1 of 2 We are given a system of two linear equations We write each of the equations in a slopeintercept form, y = k x b y=kxb y = k x b 3 x − 2 y = 8 3 x − 2 y − 3 x = 8 − 3 x − 2 y = − 3 x 8 y = 3 2 x − 4 \begin {gather*} \color {#c} 3x2y=8\\ \color {#c} 3x2y3x=x \\ \color {#See the answer (a) f (x) = 3x 5 √ x − 12 √4 x 3 x 3 x (b) y = (3x ^6 − 2x ^3 8x ^2 5) (x ^5 − x ^2 2x − 8) (c) f (t) = t^7 3t − 5/ t ^2 − 5t (d) P (x) = 7/6 (2x ^5 − 3x − 4)^12 Find the first and second derivatives of each




Factor The Following Polynomials X 2 3x 4 2x 2 Chegg Com




X 3 X 2 3x 7 2x 3 Mathematics Topperlearning Com Yrt



0 件のコメント:
コメントを投稿